Solving variant sudoku in MiniZinc
It’s straightforward to model and solve a Sudoku puzzle using MiniZinc. But the modern Sudoku world (as can be seen on the Cracking the Cryptic Youtube channel) is full of variants with exotic constraints – let’s see how hard it is to model those.
(A small disclaimer: I’m trying to model these constraints in a simple way, not necessarily an efficient way!)
Normal sudoku rules apply
The standard rules of Sudoku are easy enough: an integer variable for each of the 81 cells, constrained to take a value from 1 to 9, and each row, column, and 3x3 box required to have no duplicates (to be “all different”).
include "globals.mzn"; % to get the alldifferent constraint
% The cells of the grid.
array [1..9, 1..9] of var 1..9 : x;
% Each row is alldifferent.
constraint forall (i in 1..9) (alldifferent(x[i, 1..9]));
% Each column is alldifferent.
constraint forall (j in 1..9) (alldifferent(x[1..9, j]));
% Each 3x3 box is alldifferent.
constraint forall (i in 0..2, j in 0..2) (
alldifferent(x[3*i+1..3*i+3, 3*j+1..3*j+3])
);Some easy variants
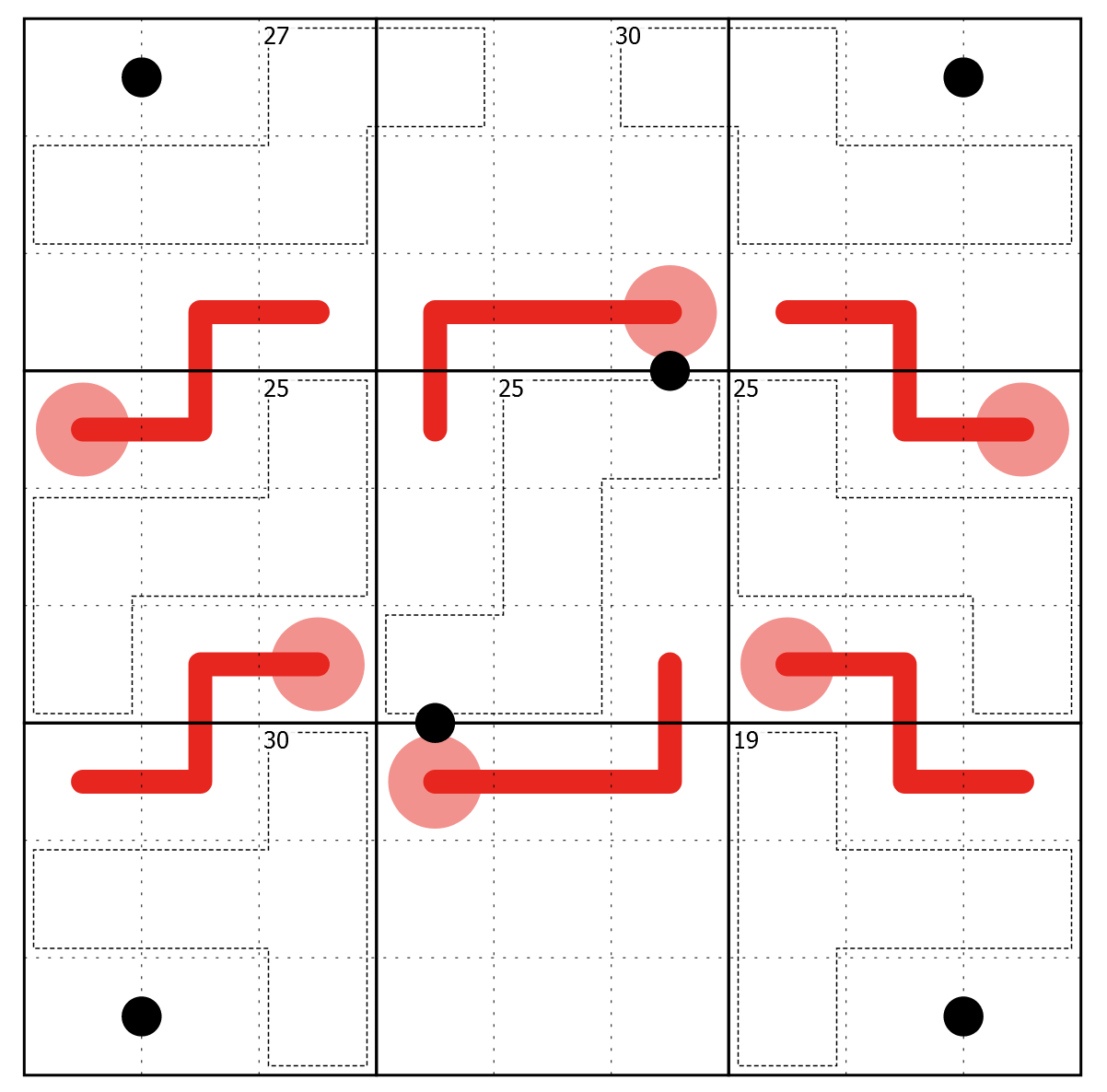
Above is our first example puzzle: Dune: The Mentat’s Diversion by HalfBakedLunatic, featured in this video.
(Little) Killer sudoku and extra regions
A killer sudoku clue requires a set of cells to sum to a given number. This is an easy case to model:
% The top-left killer clue in example puzzle 1, sum part
constraint sum([x[1,3],x[1,4],x[2,1],x[2,2],x[2,3]]) = 27;Little killer clues can be modelled the same way. Regular killer clues also require the cage to act as an extra no-duplicates region, which can be modelled simply with an alldifferent constraint:
% The top-left killer clue in example puzzle 1, no-duplicate part
constraint alldifferent([x[1,3],x[1,4],x[2,1],x[2,2],x[2,3]]);Thermometers
A thermometer requires the numbers along the line to increase from the bulb end, like the temperature markings on a thermometer. This is a conjunction of simple arithmetic constraints:
% The top-left thermometer in example puzzle 1
constraint x[4,1] < x[4,2]
/\ x[4,2] < x[3,2]
/\ x[3,2] < x[3,3];In fact MiniZinc has a global constraint that does exactly this,
called strictly_increasing:
% The top-left thermometer in example puzzle 1, again
constraint strictly_increasing([x[4,1], x[4,2], x[3,2], x[3,3]]);There’s also the constraint increasing for “slow” thermometers.
Kropki dots
Black kropki dots require one number to be double the other:
% Top-left black kropki dot in example puzzle 1
constraint (x[1,1] = x[1,2]*2) \/ (x[1,2] = x[1,1]*2)White kropki dots require the two numbers to be adjacent. There are two simple ways to write it:
% Top-left kropki dot in example puzzle 1, if we pretend it's white instead of black
constraint (x[1,1] = x[1,2]+1) \/ (x[1,2] = x[1,1]+1);
% or, state that the numbers are exactly 1 apart:
constraint abs(x[1,1] - x[1,2]) = 1;Example puzzle 1 model
These constraints can be wrapped in predicates and put together to solve example puzzle 1. Chuffed 0.13.2 solves this in just over 200ms:
include "globals.mzn";
array [1..9, 1..9] of var 1..9 : x;
constraint forall (i in 1..9) (alldifferent(x[i, 1..9]));
constraint forall (j in 1..9) (alldifferent(x[1..9, j]));
constraint forall (i in 0..2, j in 0..2) (
alldifferent(x[3*i+1..3*i+3, 3*j+1..3*j+3])
);
predicate black_kropki(var int: a, var int: b) = (a = b*2) \/ (b = a*2);
predicate thermo(array[int] of var int: xs) = strictly_increasing(xs);
predicate killer(int: clue, array[int] of var int: xs) =
alldifferent(xs) /\ sum(xs) = clue;
constraint black_kropki(x[1,1], x[1,2]);
constraint black_kropki(x[1,8], x[1,9]);
constraint black_kropki(x[3,6], x[4,6]);
constraint black_kropki(x[6,4], x[7,4]);
constraint black_kropki(x[9,1], x[9,2]);
constraint black_kropki(x[9,8], x[9,9]);
constraint killer(27, [x[1,3],x[1,4],x[2,1],x[2,2],x[2,3]]);
constraint killer(30, [x[1,6],x[1,7],x[2,7],x[2,8],x[2,9]]);
constraint killer(25, [x[4,3],x[5,1],x[5,2],x[5,3],x[6,1]]);
constraint killer(25, [x[4,5],x[4,6],x[5,5],x[6,4],x[6,5]]);
constraint killer(25, [x[4,7],x[5,7],x[5,8],x[5,9],x[6,9]]);
constraint killer(30, [x[7,3],x[8,1],x[8,2],x[8,3],x[9,3]]);
constraint killer(19, [x[7,7],x[8,7],x[8,8],x[8,9],x[9,7]]);
constraint thermo([x[4,1],x[4,2],x[3,2],x[3,3]]);
constraint thermo([x[3,6],x[3,5],x[3,4],x[4,4]]);
constraint thermo([x[4,9],x[4,8],x[3,8],x[3,7]]);
constraint thermo([x[6,3],x[6,2],x[7,2],x[7,1]]);
constraint thermo([x[7,4],x[7,5],x[7,6],x[6,6]]);
constraint thermo([x[6,7],x[6,8],x[7,8],x[7,9]]);More constraints and extra variables
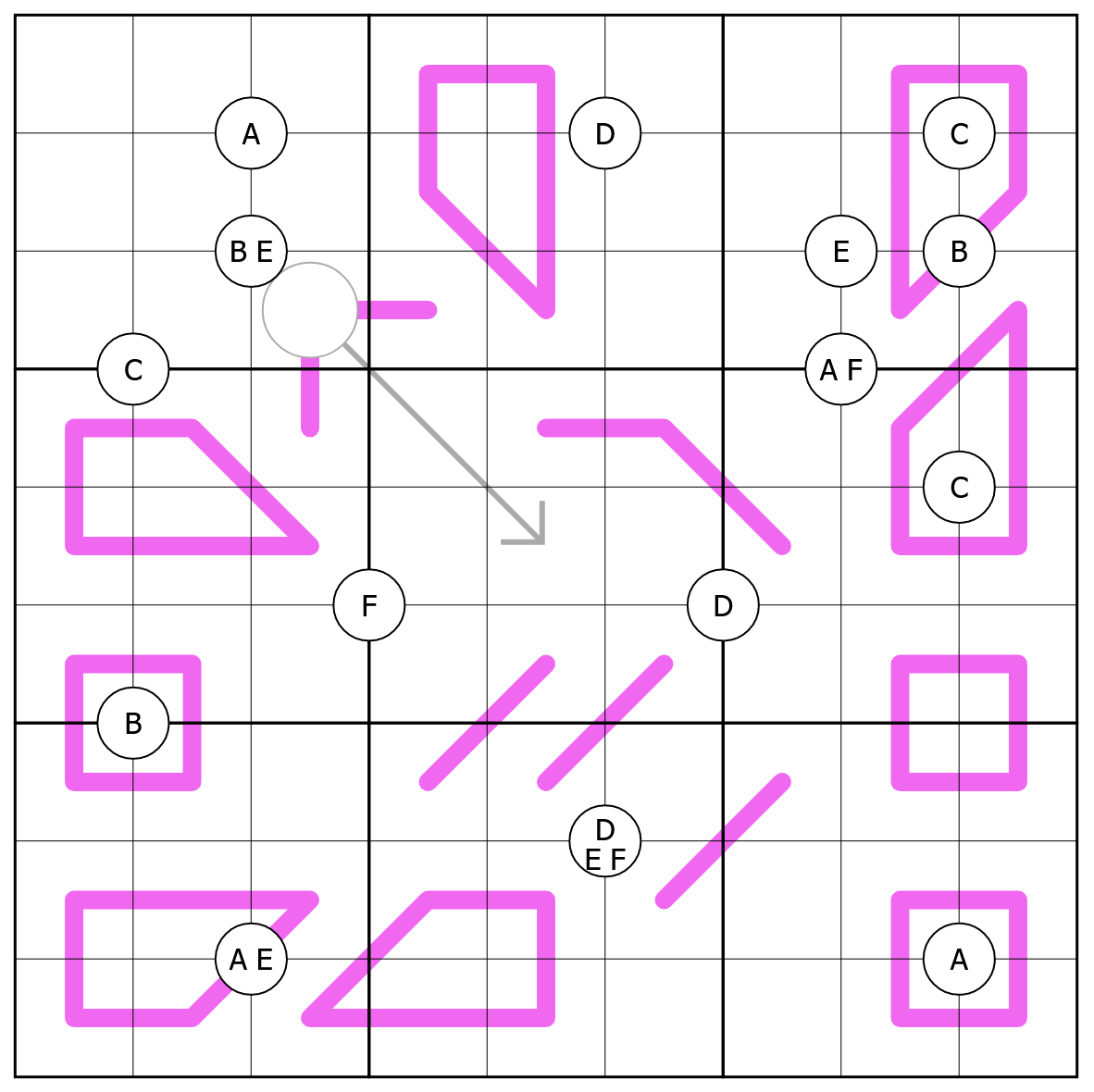
Example puzzle 2, A puzzle of two halves by Arbitrary (featured in this video).
In this puzzle the magenta lines are “renban” lines, where the digits on the line must form a set of consecutive digits without repeats. The letters A-F represent six different digits, and a letter in a circle means that letter’s digit must appear in at least one of the four surrounding cells.
The single arrow constraint is the easiest to model:
constraint x[3,3] = x[4,4]+x[5,5];The renban constraint is more complicated. We assert that all the digits along the line are different, and that the smallest and largest digit are exactly n-1 apart, where n is the number of digits on the line.
predicate renban(array[int] of var int: x) =
alldifferent(x) /\ (max(x)-min(x) = length(x)-1);To model the letters representing digits, we introduce six more variables and constrain them to be different:
var 1..9: a; var 1..9: b; var 1..9: c;
var 1..9: d; var 1..9: e; var 1..9: f;
constraint alldifferent([a,b,c,d,e,f]);For the letter-in-circle (“quad”) we assert that either the first cell
takes the given value, or the second one does, and so on. Note that
in this case the value v is not a fixed value but another variable.
% At least one of the four cells, where (i,j) is the top-left cell,
% must take the value v.
predicate quad(int: i, int: j, var int: v) =
x[i ,j ] = v
\/ x[i ,j+1] = v
\/ x[i+1,j ] = v
\/ x[i+1,j+1] = v;
% The "D E F" clue in example puzzle 2
constraint quad(7,5, d);
constraint quad(7,5, e);
constraint quad(7,5, f);Solving the model requires assigning values simultaneously to the
Sudoku cell variables in the array x and the a,b,c,d,e,f
variables. The full model, which Chuffed solves in about 270ms:
include "globals.mzn";
array [1..9, 1..9] of var 1..9 : x;
constraint forall (i in 1..9) (alldifferent(x[i, 1..9]));
constraint forall (i in 1..9) (alldifferent(x[1..9, i]));
constraint forall (i in 0..2, j in 0..2) (
alldifferent(x[3*i+1..3*i+3, 3*j+1..3*j+3])
);
constraint x[3,3] = x[4,4]+x[5,5];
predicate renban(array[int] of var int: x) =
alldifferent(x) /\ (max(x)-min(x) = length(x)-1);
constraint renban([x[1,4], x[1,5], x[2,4], x[2,5], x[3,5]]);
constraint renban([x[1,8], x[1,9], x[2,8], x[2,9], x[3,8]]);
constraint renban([x[4,1], x[4,2], x[5,1], x[5,2], x[5,3]]);
constraint renban([x[3,9], x[4,8], x[4,9], x[5,8], x[5,9]]);
constraint renban([x[8,1], x[8,2], x[8,3], x[9,1], x[9,2]]);
constraint renban([x[8,4], x[8,5], x[9,3], x[9,4], x[9,5]]);
constraint renban([x[6,1], x[6,2], x[7,1], x[7,2]]);
constraint renban([x[6,8], x[6,9], x[7,8], x[7,9]]);
constraint renban([x[8,8], x[8,9], x[9,8], x[9,9]]);
constraint renban([x[3,3], x[3,4], x[4,3]]);
constraint renban([x[4,5], x[4,6], x[5,7]]);
constraint renban([x[6,5], x[7,4]]);
constraint renban([x[6,6], x[7,5]]);
constraint renban([x[7,7], x[8,6]]);
var 1..9: a; var 1..9: b; var 1..9: c;
var 1..9: d; var 1..9: e; var 1..9: f;
constraint alldifferent([a,b,c,d,e,f]);
predicate quad(int: i, int: j, var int: v) =
x[i,j] = v \/ x[i,j+1] = v \/ x[i+1,j] = v \/ x[i+1,j+1] = v;
constraint quad(1,2, a);
constraint quad(1,5, d);
constraint quad(8,1, c);
constraint quad(2,2, b);
constraint quad(2,2, e);
constraint quad(2,7, e);
constraint quad(2,8, b);
constraint quad(3,1, c);
constraint quad(3,7, a);
constraint quad(3,7, f);
constraint quad(4,8, c);
constraint quad(5,3, f);
constraint quad(5,6, d);
constraint quad(6,1, b);
constraint quad(7,5, d);
constraint quad(7,5, e);
constraint quad(7,5, f);
constraint quad(8,2, a);
constraint quad(8,2, e);
constraint quad(8,8, a);Conditional constraints and finding connected regions
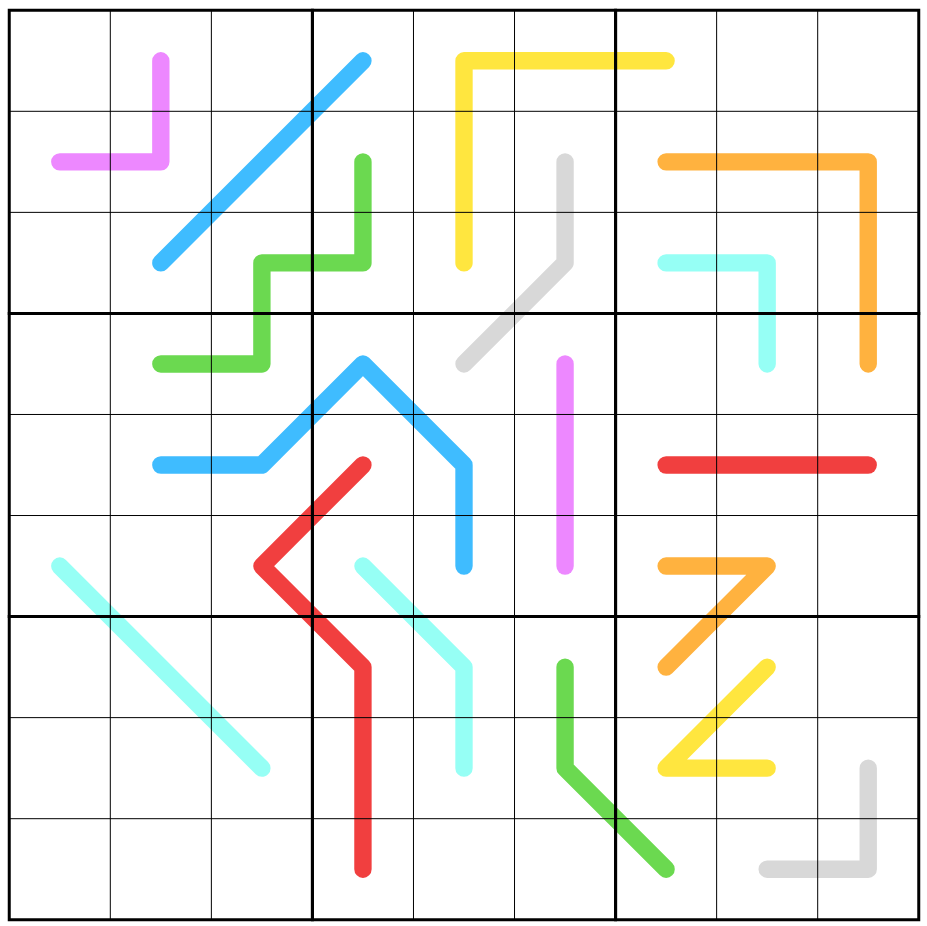
Example puzzle 3, Zippery When Wet by Marty Sears (featured in this video).
This puzzle is quite a bit more difficult, both to solve by hand and model in MiniZinc. It has a great variety of constraints and requires us to cover the grid in land and water. These are the rules, from the SudokuPad link where you can play the puzzle:
YIN-YANG:
• Each cell is either land or water.
• All cells of the same type must be orthogonally connected.
• No 2x2 area may be entirely land or entirely water.
LINE TYPES:
• Renban (pink) - Digits on a pink line don't repeat, and form a consecutive sequence, but these can be arranged in any order along the line.
• Nabner (yellow) - A digit on a yellow line cannot be consecutive with (or the same as) any other digit anywhere on the line.
• German Whisper (green) - Adjacent digits on a green line must have a difference of at least 5.
• Region Sum (blue) - Digits along a blue line must have the same total within each 3x3 box.
• Parity (red) - Digits along a red line must alternate between odd and even.
• Entropic (orange) - Any group of 3 adjacent digits on an orange line must contain a low digit (1, 2 or 3), a medium digit (4, 5 or 6), and a high digit (7, 8 or 9).
• Palindrome (grey) - A grey line must read the same in either direction.
• Same Difference (turquoise) - Each pair of adjacent digits along a turquoise line must have the same difference.
ZIPPERY WHEN WET:
• Any line that is completely wet (only enters water cells) loses the property of its presenting colour, and instead becomes a zipper line. Along a zipper line, each pair of digits that are the same distance from the line's central cell, sum to the digit in that centre cell.
• Any line that is completely dry (only enters land cells) behaves normally, as described in the list above. It does not behave like a zipper line.
• If a line is partly dry and partly wet, it retains its presenting property, but it is ALSO a zipper line as well.
New constraints
Most of the line constraints are easy to model; here are two examples:
% Zipper constraint
predicate zipper(array[int] of var int: a) =
let { int : n = length(a);
int : m = (n div 2) + 1 } in
forall (i in 1..m-1) ( a[i] + a[n-i+1] = a[m] );
% German whisper constraint.
predicate german(array[int] of var int: a) =
forall (i in 1..length(a)-1) ( abs(a[i]-a[i+1]) >= 5 );Yin-yang (land and water)
The requirement to find two connected regions is another story. The first part is easy enough; introduce Boolean variables to enforce that each cell is either land or water, and that there are no 2x2 blocks all of the same type:
% Each cell is either land or water.
array [1..9, 1..9] of var bool : land;
array [1..9, 1..9] of var bool : water;
constraint forall (i,j in 1..9) ( land[i,j] != water[i,j] );
% No 2x2 blocks of all-land or all-water.
constraint forall (i,j in 1..8) (
sum([land[i,j],land[i+1,j],land[i,j+1],land[i+1,j+1]]) in {1,2,3}
);The tricky part is ensuring that all water (or land) cells are connected. To do this we arbitrarily assign one cell as the “source” cell, and imagine that the water flows from that cell into the other cells. We have a variable for each water cell’s distance from that source cell, and assert that if a cell has distance D from the source, one of its neighbouring water cells must have distance D - 1. This ensures that there is some path from each cell back to the source cell, and therefore that all cells are connected.
% The ugliest but most important part of the Yin-Yang constraint:
% ensuring dist[i,j] represents the length of some path back to
% the source cell.
constraint forall (i,j in 1..9) (
if [i,j] = [wi,wj] then dist[i,j] = 0 % Source cell has distance zero
elseif [i,j] = [li,lj] then dist[i,j] = 0 % Source cell has distance zero
else % If our distance is D, there must exist a neigbour, of the same type,
% with distance D-1.
( ((land[i-1,j]=land[i,j]) /\ dist[i-1,j] = dist[i,j]-1) :: maybe_partial
\/ ((land[i+1,j]=land[i,j]) /\ dist[i+1,j] = dist[i,j]-1) :: maybe_partial
\/ ((land[i,j-1]=land[i,j]) /\ dist[i,j-1] = dist[i,j]-1) :: maybe_partial
\/ ((land[i,j+1]=land[i,j]) /\ dist[i,j+1] = dist[i,j]-1) :: maybe_partial )
endif
);We also add constraints to choose (arbitrarily) the top-left-most cell as the source cell, and force each cell’s distance value to be the smallest possible value. These constraints eliminate redundant solutions and reduce the search space.
Conditional constraints
The “zippery when wet” condition is then no problem:
% A clue in the puzzle translates to two conditional constraints:
% "zippery when wet" and "ordinary when dry"
predicate purple(array[int,int] of int: coords) =
(wet(coords) -> zipper(extract(x, coords)))
/\ (dry(coords) -> renban(extract(x, coords)));For the purple line, it means: if it’s a bit wet it must act as
a zipper line, and if it’s a bit dry then it must act as a renban
line. The wet and dry predicates check if any cell of the given
coordinates is water or land.
Example puzzle 3 full model
The full model below finds the solution in 1.2 seconds. One curiosity is that including the “shortest distance” constraint – intended to eliminate redundant solutions and potentially improve performance – makes the solving slower by about half a second.
include "globals.mzn";
array [1..9, 1..9] of var 1..9 : x;
constraint forall (i in 1..9) (alldifferent(x[i, 1..9]));
constraint forall (i in 1..9) (alldifferent(x[1..9, i]));
constraint forall (i in 0..2, j in 0..2) (
alldifferent(x[3*i+1..3*i+3, 3*j+1..3*j+3])
);
% Each cell is either land or water.
array [1..9, 1..9] of var bool : land;
array [1..9, 1..9] of var bool : water;
constraint forall (i,j in 1..9) ( land[i,j] != water[i,j] );
% No 2x2 blocks of all-land or all-water.
constraint forall (i,j in 1..8) (
sum([land[i,j],land[i+1,j],land[i,j+1],land[i+1,j+1]]) in {1,2,3}
);
% Location of "source" water and land cells.
var 1..9 : wi; var 1..9 : wj; constraint water[wi,wj];
var 1..9 : li; var 1..9 : lj; constraint land[li,lj];
% Shortest distance from source cell.
array [1..9, 1..9] of var 0..80 : dist;
% Constrain source water cell to be "earliest" position.
constraint forall (i,j in 1..9) (
if i < wi \/ (i==wi /\ j < wj) then water[i,j] = false else true endif
);
% Constrain source land cell to be "earliest" position.
constraint forall (i,j in 1..9) (
if i < li \/ (i==li /\ j < lj) then land[i,j] = false else true endif
);
constraint forall (i,j in 1..9) (
if [i,j] = [wi,wj] then dist[i,j] = 0 % Source cell has distance zero
elseif [i,j] = [li,lj] then dist[i,j] = 0 % Source cell has distance zero
else % If our distance is D, there must exist a neigbour, of the same type,
% with distance D-1.
( ((land[i-1,j]=land[i,j]) /\ dist[i-1,j] = dist[i,j]-1) :: maybe_partial
\/ ((land[i+1,j]=land[i,j]) /\ dist[i+1,j] = dist[i,j]-1) :: maybe_partial
\/ ((land[i,j-1]=land[i,j]) /\ dist[i,j-1] = dist[i,j]-1) :: maybe_partial
\/ ((land[i,j+1]=land[i,j]) /\ dist[i,j+1] = dist[i,j]-1) :: maybe_partial )
endif
);
% Force dist to be the shortest distance (to eliminate potential redundant solutions).
constraint forall (i,j in 1..9) (
if j<9 /\ land[i,j] = land[i,j+1] then abs(dist[i,j] - dist[i,j+1]) <= 1 endif
/\ if i<9 /\ land[i,j] = land[i+1,j] then abs(dist[i,j] - dist[i+1,j]) <= 1 endif
);
% Puzzle clues.
constraint purple([|2,1|2,2|1,2|]);
constraint purple([|4,6|5,6|6,6|]);
constraint yellow([|1,7|1,6|1,5|2,5|3,5|]);
constraint yellow([|7,8|8,7|8,8|]);
constraint red([|5,4|6,3|7,4|8,4|9,4|]);
constraint red([|5,7|5,8|5,9|]);
constraint grey([|2,6|3,6|4,5|]);
constraint grey([|8,9|9,9|9,8|]);
constraint green([|2,4|3,4|3,3|4,3|4,2|]);
constraint green([|7,6|8,6|9,7|]);
constraint cyan([|3,7|3,8|4,8|]);
constraint cyan([|6,1|7,2|8,3|]);
constraint cyan([|6,4|7,5|8,5|]);
constraint blue([|1,4|2,3|3,2|]);
constraint blue([|5,2|5,3|4,4|5,5|6,5|]);
constraint orange([|2,7|2,8|2,9|3,9|4,9|]);
constraint orange([|6,7|6,8|7,7|]);
% A clue in the puzzle translates to two conditional constraints:
% "zippery when wet" and "ordinary when dry"
predicate purple(array[int,int] of int: coords) =
(wet(coords) -> zipper(extract(x, coords))) /\ (dry(coords) -> renban(extract(x, coords)));
predicate yellow(array[int,int] of int: coords) =
(wet(coords) -> zipper(extract(x, coords))) /\ (dry(coords) -> nabner(extract(x, coords)));
predicate red(array[int,int] of int: coords) =
(wet(coords) -> zipper(extract(x, coords))) /\ (dry(coords) -> parity(extract(x, coords)));
predicate grey(array[int,int] of int: coords) =
(wet(coords) -> zipper(extract(x, coords))) /\ (dry(coords) -> palindrome(extract(x, coords)));
predicate green(array[int,int] of int: coords) =
(wet(coords) -> zipper(extract(x, coords))) /\ (dry(coords) -> german(extract(x, coords)));
predicate cyan(array[int,int] of int: coords) =
(wet(coords) -> zipper(extract(x, coords))) /\ (dry(coords) -> equidiff(extract(x, coords)));
predicate blue(array[int,int] of int: coords) =
(wet(coords) -> zipper(extract(x, coords))) /\ (dry(coords) -> regionsum(coords));
predicate orange(array[int,int] of int: coords) =
(wet(coords) -> zipper(extract(x, coords))) /\ (dry(coords) -> entropic(extract(x, coords)));
% A line is "wet" if any of its cells are water.
predicate wet(array[int,int] of int: coords) = exists(extract(water, coords));
% A line is "dry" if any of its cells are land.
predicate dry(array[int,int] of int: coords) = exists(extract(land, coords));
% Extract a set of variables with given coordinates from a 2d array of variables.
function array[int] of var $T : extract(array[int,int] of var $T : v, array[int,int] of int: cs) =
[ v[cs[c,1],cs[c,2]] | c in index_set_1of2(cs) ];
% Zipper constraint
predicate zipper(array[int] of var int: a) =
let { int : n = length(a);
int : m = (n div 2) + 1 } in
forall (i in 1..m-1) ( a[i] + a[n-i+1] = a[m] );
% Renban constraint
predicate renban(array[int] of var int: a) =
alldifferent(a) /\ (max(a)-min(a) = length(a)-1);
% Nabner constraint
predicate nabner(array[int] of var int: a) =
forall(i,j in index_set(a) where i<j) (abs(a[i]-a[j]) >= 2);
% Parity (odd-even) constraint
predicate parity(array[int] of var int: a) =
forall (i in 1..length(a)-1) ( a[i] mod 2 != a[i+1] mod 2 );
% Palindrome constraint.
predicate palindrome(array[int] of var int: a) =
let { int : n = length(a);
int : m = (n div 2) + 1 } in
forall (i in 1..m-1) ( a[i] = a[n-i+1] );
% German whisper constraint.
predicate german(array[int] of var int: a) =
forall (i in 1..length(a)-1) ( abs(a[i]-a[i+1]) >= 5 );
% Equal-difference constraint.
predicate equidiff(array[int] of var int: a) =
forall (i in 1..length(a)-2) ( abs(a[i]-a[i+1]) = abs(a[i+1]-a[i+2]) );
% Region-sum constraint.
predicate regionsum(array[int,int] of int: coords) =
% Introduce the "sum value" for this line.
let { var int : sum } in
% Start walking the line.
regionsum2(coords, x[coords[1,1],coords[1,2]], sum, 2);
predicate regionsum2(array[int,int] of int : coords, var int : runningsum, var int : sum, int : i) =
% At the end of the line, close the current box.
if i > card(index_set_1of2(coords)) then runningsum = sum
% We've crossed a box border, so close the current box and recurse with a new running sum.
elseif box(coords[i,1],coords[i,2]) != box(coords[i-1,1],coords[i-1,2])
then runningsum = sum /\ regionsum2(coords, x[coords[i,1],coords[i,2]], sum, i+1)
% We're still in the same box, so just add to the running sum.
else regionsum2(coords, x[coords[i,1],coords[i,2]]+runningsum, sum, i+1)
endif;
% Map coordinate -> box number.
function int: box(int: i,int: j) = ((i-1) div 3) * 3 + ((j-1) div 3) + 1;
% Entropic line constraint.
predicate entropic(array[int] of var int : a) =
forall(i in 1..length(a)-2) (
(a[i]-1) div 3 != (a[i+1]-1) div 3
/\ (a[i]-1) div 3 != (a[i+2]-1) div 3 );
solve satisfy;
output [show(x[i,j]) ++ if j=9 then "\n" else "" endif | i,j in 1..9];
output [if fix(water[i,j]) then "~" else "#" endif ++ if j=9 then "\n" else "" endif | i,j in 1..9];