Template Haskell for faster linear interpolation
An application I’m writing requires a lot of linear interpolation of a function. There’s so much of it, in fact, that it was the biggest single contributor to the running time. In this article I show how I used Template Haskell to make it much faster and cut the overall running time of the application by about a third.
To be clear about the problem, we have a list of points (which I’ll call the “table”) like this:
(0.00, 0.00)
(0.50, 0.48)
(1.00, 0.84)
(1.50, 1.00)
(2.00, 0.91)
(2.50, 0.60)
(3.00, 0.14)
(3.50, -0.35)
(4.00, -0.76)
(4.50, -0.98)
(5.00, -0.96)
(5.50, -0.71)
(6.00, -0.28)
(6.50, 0.22)
(7.00, 0.66)
(7.50, 0.94)
(8.00, 0.99)
(8.50, 0.80)
(9.00, 0.41)
(9.50, -0.08)
(10.00, -0.54)These points are input-output pairs for some function f, and we want
to define the points in the middle by joining the dots with straight
lines. For example, since f(0.5) = 0.4 and f(1.0) = 0.84, we want to
have that f(0.75) = 0.66 because it’s halfway between those two points.
So, for a given input value x, we have to find the two points (a,av)
and (b,bv) such that x is between a and b, and the result should
be calculated like this:
-- Compute the linear interpolation of "x" between the points (a,av)
-- and (b,bv).
interpolate (a,av) (b,bv) x = av + (x-a)*(bv-av)/(b-a)All we need to do is find those two neighbouring points. For any
values that are outside of the range of the table, we just use the
nearest value; e.g. for the sample table above, f(100) = -0.54.
Linear lookup
A lot of the time, you might write a simple linear traversal of the table like this and call it a day:
-- Ordinary linear traversal of the table.
linearLookup :: [ (Double,Double) ] -> Double -> Double
linearLookup [] x = error "linearLookup: empty table"
linearLookup ((a,av):rest) x | x <= a = av
| otherwise = loop ((a,av):rest)
where -- At the end of the table, so use the last value.
loop [(a,av)] = av
loop ((a,av):(b,bv):rest)
-- We've found the target range; do the interpolation.
| x <= b = interpolate (a,av) (b,bv) x
-- Otherwise, keep looking.
| otherwise = loop ((b,bv):rest)When I was writing the application in question, I was struck by the feeling that this was not “Haskelly” enough – there’s direct recursion, and it doesn’t even have any monoids. So I wrote this instead:
-- Use the First monoid to "hide" the recursion.
monoidalLookup :: [ (Double, Double) ] -> Double -> Double
monoidalLookup table x =
case (firstJust . map f . tails) table of
Just (ap,bp) -> interpolate ap bp x
Nothing -> if x < fst (head table)
then snd (head table)
else snd (last table)
where f ((a,av):(b,bv):_) | a <= x && x <= b = Just ((a,av),(b,bv))
f _ = Nothing
-- Get the first "Just" value from a list.
firstJust :: [Maybe a] -> Maybe a
firstJust = getFirst . mconcat . map FirstIt’s the same linear-traversal strategy, but written so that it’s harder to understand. (It occurred to me in writing this article that it might be clearer to use a fold directly instead of the First monoid, but I didn’t try this.) The only thing you could say in its defense is that the “selection” part (called “f” there) is separated from the rest of the algorithm.
Map lookup
A linear traversal is simple, but has the drawback that to get to
values near the end of the table we have to traverse the whole table.
Profiling my application suggested that this monoidal lookup was
spectacularly slow. Maybe we can use a Map instead?
-- Find the points to interpolate between using a map.
mapLookup :: Map Double Double -> Double -> Double
mapLookup m x =
case (lookupLE x m, lookupGE x m) of
(Just (a,av), Just (b,bv)) ->
if a == b
then av
else interpolate (a,av) (b,bv) x
(Nothing, Just (b,bv)) -> bv
(Just (a,av), Nothing) -> av
_ -> error "mapLookup"The first argument to mapLookup is just the table converted to a
Map; e.g. Data.Map.fromList table. This approach reduces the
worst case from \(O(N)\) to \(O(\log N)\), but hurts the best case and
introduces some overhead in general. It also seems a bit inefficient
to do two lookups (the lookupLE and lookupGE) when they are both
really looking for the same spot in the tree.
In my application, I used this mapLookup function for a long time,
until improvements in other parts of the program meant that
interpolation was again the bottleneck.
My next approach was to encode the lookup as a series of <= / >
comparisons, essentially the same as how a Map would work
internally. The table is encoded as a tree, where each entry in the
table becomes a node with two children, or a leaf.
data SplitTree = Leaf
| Node (Double, Double) SplitTree SplitTree
deriving (Show)
makeTree :: [(Double,Double)] -> SplitTree
makeTree [] = Leaf
makeTree [p] = Node p Leaf Leaf
makeTree ps = let n = length ps
m = n `div` 2
(left, (middle:right)) = splitAt m ps
in Node middle (makeTree left) (makeTree right)The makeTree function turns a table into a tree, evenly distributing
the table entries to the left and right. Doing the lookup is similar
to a standard binary search, with the addition of keeping track of the
most recent times we took left and right branches.
treeLookup :: SplitTree -> Double -> Double
treeLookup t x = loop Nothing Nothing t
where
loop lb ub Leaf =
case (lb,ub) of
(Nothing, Nothing) -> error "can't interpolate on empty tree"
(Just (l,lv), Nothing) -> lv
(Nothing, Just (u,uv)) -> uv
(Just (l,lv), Just (u,uv)) -> interpolate (l,lv) (u,uv) x
loop lb ub (Node (n,nv) left right) =
case compare x n of
EQ -> nv
LT -> loop lb (Just (n,nv)) left
GT -> loop (Just (n,nv)) ub rightStatic Compilation
The point of the treeLookup function above is that we can easily
“unroll” the loop, turning it into a series of nested comparisons.
For example, for the simple table [(1,1), (2,4), (3,9)], we’d like
to get as a result a function like this:
littleLookup x =
case compare x 2 of
EQ -> 4
LT -> case compare x 1 of
EQ -> 1
LT -> 1
GT -> 1 + (((x - 1) * (4 - 1)) / (2 - 1))
GT -> case compare x 3 of
EQ -> 9
LT -> 4 + (((x - 2) * (9 - 4)) / (3 - 2))
GT -> 9The nice thing is that via Template Haskell we can do this with only
some small modification of the treeLookup function above. The
structure of the function stays essentially the same; the main work is
in annotating which parts should be evaluated statically, and which
parts are in the resulting “unrolled” function.
unrollLookupTree :: SplitTree -> ExpQ
unrollLookupTree t = do
x <- newName "x"
body <- loop (varE x) Nothing Nothing t
return $ LamE [VarP x] body
loop :: ExpQ -> Maybe (Double,Double) -> Maybe (Double,Double)
-> SplitTree -> ExpQ
loop x lb ub Leaf =
case (lb,ub) of
(Nothing, Nothing) -> error "can't interpolate on empty tree"
(Just (l,lv), Nothing) -> ld lv
(Nothing, Just (u,uv)) -> ld uv
(Just (l,lv), Just (u,uv)) ->
[| $(ld lv) + ($x - $(ld l)) * ($(ld uv) - $(ld lv))
/ ($(ld u) - $(ld l)) |]
loop x lb ub (Node (n,nv) left right) =
[| case compare $x $(ld n) of
EQ -> $(ld nv)
LT -> $(loop x lb (Just (n,nv)) left)
GT -> $(loop x (Just (n,nv)) ub right)
|]
-- Lift a Double to an ExpQ
ld :: Double -> ExpQ
ld = litE . rationalL . realToFracOne hiccup is that Template Haskell won’t automatically lift a
Double value to an expression — apparently, only integers and
rationals are allowed. As a consequence I used the little function
ld to turn a Double into a rational literal.
You can also unroll the linear lookup version:
unrollLinearLookup [] = error "linearLookup: empty table"
unrollLinearLookup table = do
x <- newName "x"
body <- linearLoop (varE x) Nothing table
return $ LamE [VarP x] body
linearLoop :: ExpQ -> Maybe (Double,Double)
-> [(Double,Double)] -> ExpQ
linearLoop x Nothing [] = error "absolutely cannot happen"
linearLoop x (Just (a,av)) [] = ld av
linearLoop x previous ((b,bv):rest) =
let val = case previous of
Just (a,av) ->
[| $(ld av) + ($x - $(ld a)) * ($(ld bv) - $(ld av))
/ ($(ld b) - $(ld a)) |]
Nothing -> ld bv
in [| case compare $x $(ld b) of
GT -> $(linearLoop x (Just (b,bv)) rest)
_ -> $val
|]Performance Comparison
We could debate which of these methods is the most elegant, but at least we can easily address the question of which one is the fastest.
(If you want to see the full source code to reproduce these results, or just for fun, see this repository on GitHub.)
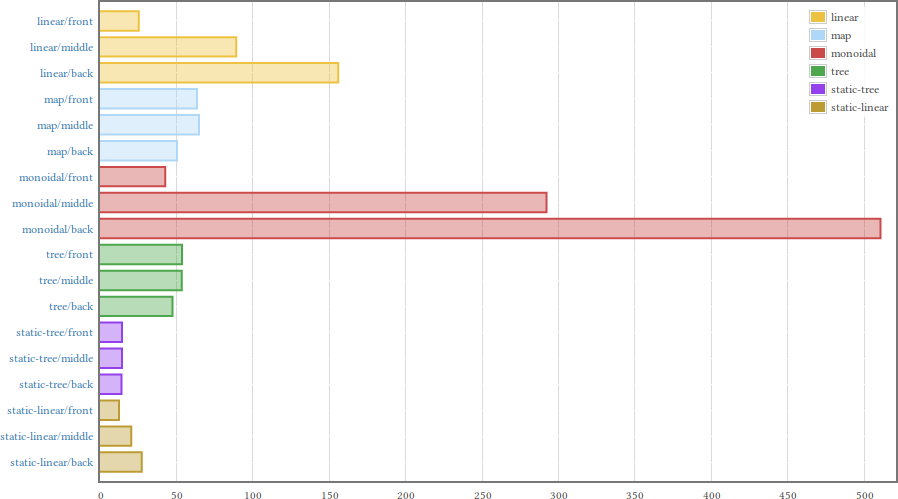
I measured each method, looking up a value at the start, middle and end of the table; the table has 21 entries. Here are the results, courtesy of the criterion library:
(Click on the image above to get the full report and all the exciting details.) As we expected, linear lookups are fast when the target is at the front, but get slower as the target gets towards the end. Also, the binary lookups take about the same time no matter where the target is.
The monoidal lookup is impressively inefficient. The statically unrolled lookups are noticeably faster than their regular versions, so it’s a worthwhile transformation if the table is known at compile time.
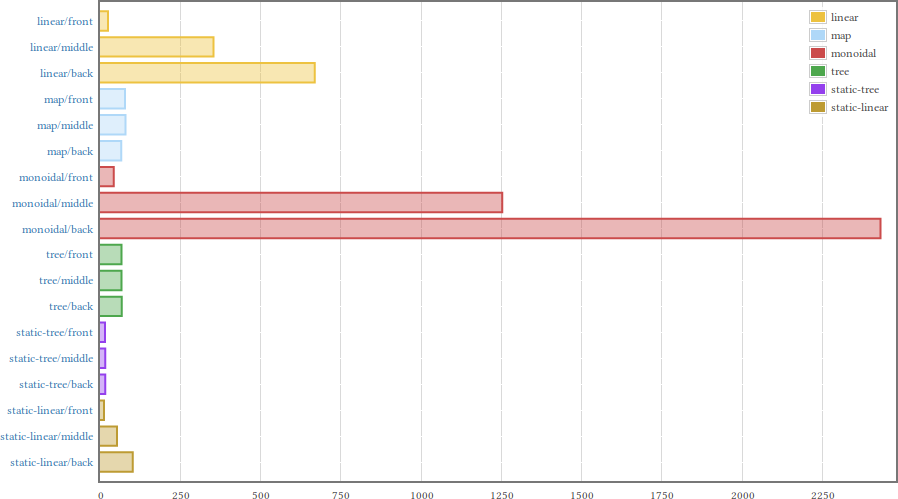
For a bigger table (101 entries) the results are basically the same, but with the end-of-the-table-linear-lookup effect magnified. Note that the scale on the horizontal axis has changed.
Finally, I measured the effect that actually matters: how much faster
my application runs. Here is a short sample run using the mapLookup
function with some GHC and timing statistics:
2,743,929,608 bytes allocated in the heap
[...]
MUT time 2.55s ( 2.64s elapsed)
GC time 0.33s ( 0.26s elapsed)
[...]
Total time 2.88s ( 2.91s elapsed)
[...]
./SimpleMain newp02-bin +RTS -s 2.89s user 0.02s system 99% cpu 2.912 total
And using the statically unrolled tree lookup:
974,367,480 bytes allocated in the heap
[...]
MUT time 1.70s ( 1.72s elapsed)
GC time 0.20s ( 0.20s elapsed)
[...]
Total time 1.90s ( 1.92s elapsed)
[...]
./SimpleMain newp02-bin +RTS -s 1.90s user 0.02s system 99% cpu 1.922 total
There’s a reduction in allocation, but more importantly the running time of the program as a whole is reduced by about one third.
Conclusion
In the end this was a worthwhile exercise: I got a faster program and learnt about Template Haskell along the way.
Whether the same trick is useful in other places depends on the circumstances. The static compilation of the lookup was only useful because it is called so very often – maybe the algorithm could be changed at a higher level to avoid making so many lookups.